Minimum spanning trees (MST) & Floodfill

por Ariel Parra

Algoritmo de Kruskal para Minimum spanning trees (MST)

En el algoritmo de Kruskal, el spanning tree inicial solo contiene los nodos del grafo y no contiene ninguna arista (vertices). Luego, el algoritmo recorre las aristas ordenadas por sus pesos y siempre agrega una arista al árbol si no crea un ciclo. El algoritmo mantiene los componentes del árbol. Inicialmente, cada nodo del grafo pertenece a un componente separado. Siempre que se agrega una arista al árbol, se unen dos componentes. Finalmente, todos los nodos pertenecen al mismo componente y se ha encontrado un árbol de expansión mínimo (Minimum spanning tree).

Ahora apliquemos el algoritmo a este grafo:

#c

CPC Γα=Ω5

El grafo contiene 9 vértices y 14 aristas. Por lo tanto, el árbol de expansión mínima formado tendrá (9 - 1) = 8 aristas. Después de ordenar queda como:

Weight Source Destination
1 7 6
2 8 2
2 6 5
4 0 1
4 2 5
6 8 6
7 2 3
7 7 8
8 0 7
8 1 2
9 3 4
10 5 4
11 1 7
14 3 5

Ahora selecciona todas las aristas una por una de la lista ordenada de aristas.

CPC Γα=Ω5
Paso 1: Seleccione la arista 7-6. No se forma ningún ciclo, incluirlo.

#c

Paso 2: Seleccione el borde 8-2. No se forma ningún ciclo, incluirlo.

#c

CPC Γα=Ω5
Paso 3: Seleccione la arista 6-5. No se forma ningún ciclo, incluirlo.

#c

Paso 4: Seleccione la arista 0-1. No se forma ningún ciclo, incluirlo.

#c

CPC Γα=Ω5
Paso 5: Seleccione el borde 2-5. No se forma ningún ciclo, .

#c

Paso 6: Seleccione la arista 8-6. Como incluir esta arista genera el ciclo, deséchela. Seleccione la arista 2-3: no se forma ningún ciclo, incluirlo.

#c

CPC Γα=Ω5

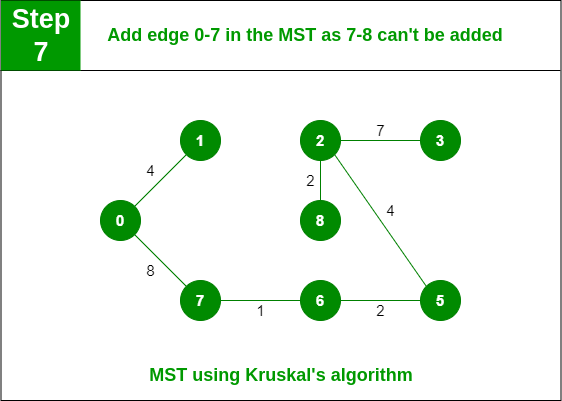
Paso 7: Seleccione la arista 7-8. Como incluir esta arista genera un ciclo, deséchela. Seleccione la arista 0-7. No se forma ningún ciclo, incluirlo.

#c

Paso 8: Seleccione la arista 1-2. Dado que incluir esta arista genera el ciclo, deséchela. Seleccione la arista 3-4. No se forma ningún ciclo, incluirlo.

#c

El número de aristas en el MST es (V – 1), y sale.

CPC Γα=Ω5

Implementacion

// Find function for DSU (Disjoint Set Union) with path compression
int find(int i, vector<int>& parent) {
    if (parent[i] == -1) return i;
    return parent[i] = find(parent[i], parent);
}// complejidad amortizada O(α(n)) , casi constante O(1)
// Union function for DSU (Disjoint Set Union) with union
void unite(int x, int y, vector<int>& parent, vector<int>& rank) {
    int s1 = find(x, parent); int s2 = find(y, parent);

    if (s1 != s2) {
        if (rank[s1] < rank[s2]) {
            parent[s1] = s2;
        } else if (rank[s1] > rank[s2]) {
            parent[s2] = s1;
        } else {
            parent[s2] = s1;
            rank[s1]++;
        }
    }
}// complejidad amortizada O(α(n)) , casi constante O(1)
CPC Γα=Ω5
void kruskals_mst(int V, vector<vector<int>>& edgelist) {
    // Sort all edges by weight
    sort(edgelist.begin(), edgelist.end()); // O(E log E)

    vector<int> parent(V, -1);
    vector<int> rank(V, 1);
    int ans = 0;

    cout << "Following are the edges in the constructed MST" << endl;
    for (auto& edge : edgelist) {
        int w = edge[0];
        int x = edge[1];
        int y = edge[2];

        // Take this edge in MST if it does not form a cycle
        if (find(x, parent) != find(y, parent)) {
            unite(x, y, parent, rank);
            ans += w;
            cout << x << " -- " << y << " == " << w << endl;
        }
    }
    cout << "Minimum Cost Spanning Tree: " << ans << endl;
}//O(E log E) ≈ O(E log V)
CPC Γα=Ω5

Floodfill

es un algoritmo que identifica y etiqueta el componente conectado al que pertenece una celda en particular, en una matriz multidimensional. Básicamente, es DFS o BFS, pero en una cuadrícula, y queremos encontrar el componente conectado de todas las celdas conectadas con el mismo número.

#c

CPC Γα=Ω5

Implementacion con BFS

// Fill the image img[x][y] and all its same colored
// adjacent with the given new color
void floodFill(vector<vector<int>>& img, int x, int y, int newClr){                    
    queue<pair<int, int>> q;

    // Rows and columns of the display
    int m = img.size();
    int n = img[0].size();
   
    //save some unnecessary recursive calls for the adjacent of the last nodes
    int prevClr = img[x][y];
    if (prevClr == newClr) return;

    // Append the position of starting pixel
    // of the component
    q.push({x, y});
    img[x][y] = newClr;
CPC Γα=Ω5
    // While the queue is not empty i.e. the 
    // whole component having prevClr color
    // is not colored with newClr color
    while (!q.empty()) {
        // Dequeue the front node
        x = q.front().first;
        y = q.front().second;
        q.pop();
        // Check if the adjacent pixels are valid 
        // and enqueue
        if (x + 1 < m && img[x + 1][y] == prevClr) {
            img[x + 1][y] = newClr;
            q.push({x + 1, y});
        }
        if (x - 1 >= 0 && img[x - 1][y] == prevClr) {
            img[x - 1][y] = newClr;
            q.push({x - 1, y});
        }
        if (y + 1 < n && img[x][y + 1] == prevClr) {
            img[x][y + 1] = newClr;
            q.push({x, y + 1});
        }
        if (y - 1 >= 0 && img[x][y - 1] == prevClr) {
            img[x][y - 1] = newClr;
            q.push({x, y - 1});
        }
    }
} //O(m * n)
CPC Γα=Ω5
CPC Γα=Ω5

Problemas

CPC Γα=Ω5

Referencias

CPC Γα=Ω5