Geometría computacional

Por Ariel Parra,

Complex numbers

Para el manejo de números complejos en c++ existe la libreria <complex> donde dichos números complejos tienen la forma a + bi, donde a es la parte real y b la imaginaria. Por lo tanto, podemos hacer que a sea la coordenada x ỳ b coordenada y. ¡Pues los números complejos se pueden representar como vectores de 2D.

Entonces podemos definir un tipo de dato point con el cual podemos realizar operaciones de vectores necesarias para los planos.

typedef complex<double> point; // cannot be declared as integer, abs() will fail
#define x real() // or `#define x() real()` to use x as a variable
#define y imag() // or `#define y() real()` to use y as a variable
// Example
point a = 2, b(3, 7), c = {4, 2};
    cout << a << ' ' << b << ' '<< c << endl; // (2, 0) (3, 7) (4, 2)
    cout << a + b << endl;         // (5, 7)    
    cout << "ax = " << a.x << ", ay = " << a.y << endl; // ax =  2, ay = 0
CPC Γα=Ω5

Ejercicio en Clase

Dado un vector<point> v; completa la función lambda o realiza una función de tipo auto para ordenar las partes reales de dichos puntos en orden ascendente, y si dos numeros reales son iguales se tendra que ordenar los numeros imaginarios de igual manera, para después imprimir los elementos del vector.

    #define all(a) (a).begin(), (a).end() 
    typedef complex<double> point;
    vector<point> v = { {3, 4}, {1, 2}, {3, 2}, {1, 3} };

    sort(all(v), [](const point& a, const point& b) {
        return //...;
    });
    for (//...) {
        cout << "(" << p.x << ", " << p.y << ")" << endl;
    }
CPC Γα=Ω5

Solución

vector<point> v = { {3, 4}, {1, 2}, {3, 2}, {1, 3} };

    sort(all(v), [](const point& a, const point& b) {
        return a.x != b.x ? a.x < b.x : a.y < b.y;
    });
   for (const point& p: v) {
        cout << "(" << p.x << ", " << p.y << ")" << endl;
    }
    /*
    (1, 2)
    (1, 3)
    (3, 2)
    (3, 4)
    */
CPC Γα=Ω5

Points and lines

El producto cruz de dos vectores y se calcula con la fórmula:

El resultado del producto cruz puede interpretarse como:

  • Si , el vector gira hacia la izquierda con respecto a .
  • Si , los vectores son colineales y no gira respecto a .
  • Si , el vector gira hacia la derecha con respecto a .

#c

CPC Γα=Ω5

Point location

El producto cruz se puede usar para determinar si un punto está ubicado a la izquierda o derecha de una línea definida por dos puntos. Supongamos que la línea pasa por los puntos y , y estamos mirando desde hacia . Queremos determinar la posición del punto .

El cálculo se realiza con el producto cruz:

  • Si el producto cruz es positivo: el punto está ubicado a la izquierda de la línea.
  • Si el producto cruz es negativo: el punto está ubicado a la derecha de la línea.
  • Si el producto cruz es cero: los puntos , y están alineados.
CPC Γα=Ω5

Distance functions

CPC Γα=Ω5

Euclidean Distance

La distancia euclidiana mide la longitud de la línea recta entre dos puntos en un espacio n-dimensional. Para dos puntos y :

En un espacio tridimensional (, ):

CPC Γα=Ω5

Manhattan Distance

La distancia Manhattan, también conocida como distancia de "taxista" o distancia "cuadrada", mide la suma de las diferencias absolutas en cada dimensión entre dos puntos y :

En un espacio tridimensional (, ):

CPC Γα=Ω5

Point distance from a line

#c

CPC Γα=Ω5

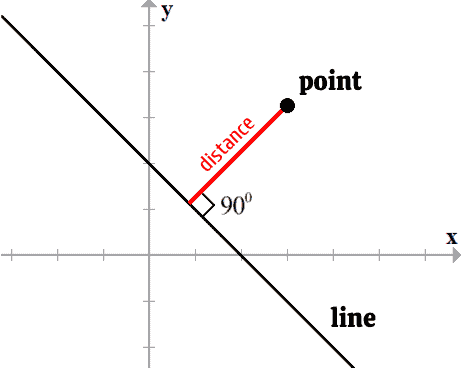
La distancia más corta entre un punto y una línea definida por los puntos y se deriva comparando el área del triángulo formado por en dos formas:

  1. El área en términos de :

    Á

  2. El área como producto cruzado:

    Á

Igualando estas dos expresiones y despejando , obtenemos:

CPC Γα=Ω5

Line segment intersection

Este problema consiste en determinar si dos segmentos de línea, y , se intersectan. Las posibles situaciones son:

Caso 1: Los segmentos están sobre la misma línea y se solapan

En este caso, hay un número infinito de puntos de intersección. Por ejemplo, en la siguiente ilustración, todos los puntos entre y son puntos de intersección:

#c

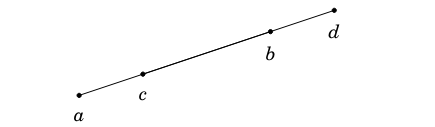
Para verificar esta situación:

  1. Usar productos cruzados para confirmar que todos los puntos están en la misma línea.
  2. Ordenar los puntos y comprobar si los segmentos se solapan.
CPC Γα=Ω5

Caso 2: Los segmentos tienen un vértice común como único punto de intersección

En este caso, el punto de intersección es exactamente uno de los vértices de los segmentos. Por ejemplo:

#c

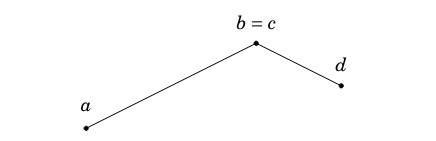
Es fácil verificar este caso, ya que solo hay cuatro posibilidades:

CPC Γα=Ω5

Caso 3: Hay un único punto de intersección que no es vértice de ningún segmento

En este caso, los segmentos se intersectan en exactamente un punto que no es vértice. Por ejemplo:

#c

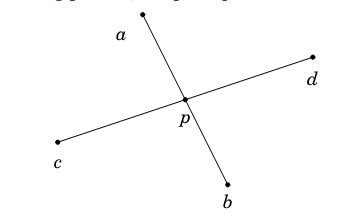
Para determinar si los segmentos se intersectan:

  1. Verificar que los puntos y están en diferentes lados de la línea a través de y .
  2. Verificar que los puntos y están en diferentes lados de la línea a través de y .

Esto se puede hacer usando productos cruzados.

CPC Γα=Ω5

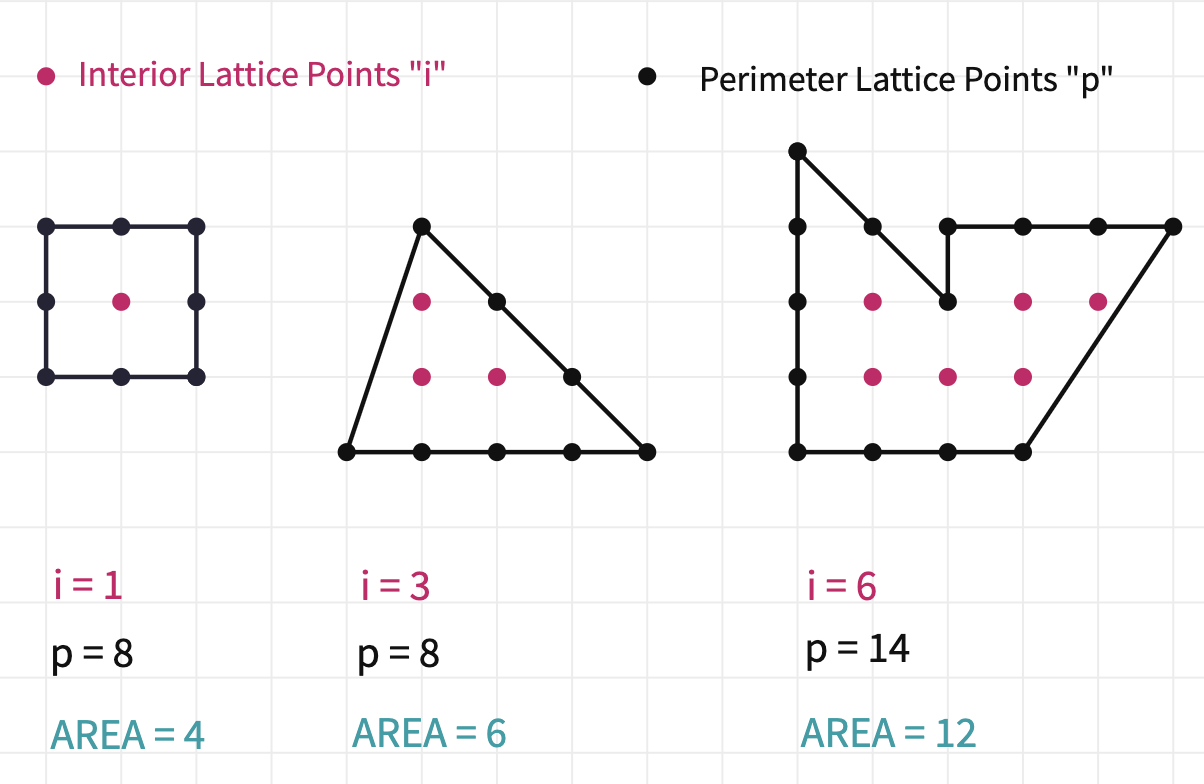
Pick’s theorem for a polygon area

El teorema de Pick proporciona una manera de calcular el área de un polígono siempre que todos los vértices del polígono tengan coordenadas enteras. Según este teorema, el área del polígono se calcula como:

Donde:

  • : es el número de puntos enteros dentro del polígono.
  • : es el número de puntos enteros en la frontera del polígono.

#c

CPC Γα=Ω5

Vector Operations using C++ Complex (point)

Given:

  • a = (2, 3)
  • b = (4, 1)
  1. Vector addition/substraction: a + b,a - b, Example: (2, 3) + (4, 1) = (2 + 4, 3 + 1) = (6, 4)
  2. Scalar multiplication/division: r * a,r / a, Example: If r = 3, then 3 * (2, 3) = (3 * 2, 3 * 3) = (6, 9)
  3. Dot product: (conj(a) * b).x, Example: (2 * 4 + 3 * 1) = 8 + 3 = 11
  4. Cross product: (conj(a) * b).y, Example: (2 * 1 - 3 * 4) = 2 - 12 = -10
  5. Squared distance: norm(a - b),Example: ((2 - 4)^2 + (3 - 1)^2) = (-2)^2 + (2)^2 = 4 + 4 = 8
  6. Euclidean distance: abs(a - b), Example: sqrt((2 - 4)^2 + (3 - 1)^2) = sqrt(8) ≈ 2.83
  7. Angle of elevation: arg(b - a), Example: atan2(1 - 3, 4 - 2) = atan2(-2, 2) = -π/4 ≈ -0.785 radians
  8. Slope of line (a, b): tan(arg(b - a)), Example: Slope = (1 - 3) / (4 - 2) = -2 / 2 = -1
CPC Γα=Ω5

Given:

  • a = (2, 3), b = (4, 1), c = (4, 1), v = (4, 1)
  • p = (3, 2)
  • theta = π / 4 (45°)
  • r = 5 (radius)

  1. Polar to cartesian: polar(r, theta)
    Example: x = r * cos(theta) = 5 * cos(π / 4) ≈ 3.54, y = r * sin(theta) = 5 * sin(π / 4) ≈ 3.54, Result: (3.54, 3.54)

  2. Cartesian to polar: point(abs(p), arg(p))
    Example: r = sqrt(3^2 + 2^2) = sqrt(9 + 4) = sqrt(13) ≈ 3.61, theta = atan2(2, 3) ≈ 0.588 radians, Result: (3.61, 0.588)

  3. Rotation about the origin: a * polar(1.0, theta)
    Example: rotated = (2 * cos(π / 4) - 3 * sin(π / 4), 2 * sin(π / 4) + 3 * cos(π / 4)) = (2 * 0.707 - 3 * 0.707, 2 * 0.707 + 3 * 0.707), Result: (-0.707, 3.536)

  4. Rotation about pivot p: (a - p) * polar(1.0, theta) + p
    Example: relative = (2 - 3, 3 - 2) = (-1, 1), rotated = (-1 * cos(π / 4) - 1 * sin(π / 4), -1 * sin(π / 4) + 1 * cos(π / 4)) = (-0.707 - 0.707, -0.707 + 0.707) = (-1.414, 0), final = (-1.414 + 3, 0 + 2) = (1.586, 2)

CPC Γα=Ω5

  1. Angle ABC: abs(remainder(arg(a - b) - arg(c - b), 2.0 * M_PI))
    Example: arg(a - b) = atan2(3 - 2, 2 - 3) = atan2(1, -1) = π / 4, arg(c - b) = atan2(1 - 2, 4 - 3) = atan2(-1, 1) = -π / 4, angle = abs(remainder(π / 4 - (-π / 4), 2π)) = abs(π / 2), Result: π / 2 ≈ 1.57 radians

  2. Project p onto vector v: v * dot(p, v) / norm(v)
    Example:dot(p, v) = 3 * 4 + 2 * 1 = 12 + 2 = 14
    norm(v) = 4^2 + 1^2 = 16 + 1 = 17
    projection = (4, 1) * (14 / 17) ≈ (3.29, 0.82)

  3. Project p onto line (a, b): a + (b - a) * dot(p - a, b - a) / norm(b - a)
    Example:
    b - a = (4 - 2, 1 - 3) = (2, -2)
    p - a = (3 - 2, 2 - 3) = (1, -1)
    dot(p - a, b - a) = 1 * 2 + (-1) * (-2) = 2 + 2 = 4
    norm(b - a) = 2^2 + (-2)^2 = 4 + 4 = 8
    projection = (2, 3) + (2, -2) * (4 / 8) = (2, 3) + (1, -1) = (3, 2)

CPC Γα=Ω5

  1. Reflect p across line (a, b): a + conj((p - a) / (b - a)) * (b - a)
    Example: a = (2, 3), b = (4, 1), p = (3, 2)
    Result: (3, 2) (reflection is identical because the point lies on the line)

  2. Intersection of line (a, b) and (p, q):

point intersection(point a, point b, point p, point q) {
  double c1 = cross(p - a, b - a), c2 = cross(q - a, b - a);
  return (c1 * q - c2 * p) / (c1 - c2); // undefined if parallel
}
CPC Γα=Ω5

Problema

CPC Γα=Ω5

Referencias

CPC Γα=Ω5

5 minutos para resolver

La Verde es Euclideana y las demas Manhattan equivalentes